176. Биссектриса угла A
треугольника ABC
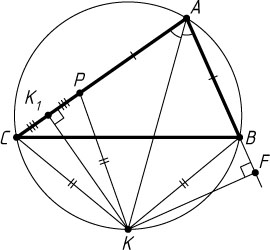
пересекает описанную около треугольника окружность в точке K
. Докажите, что проекция отрезка AK
на прямую AB
равна полусумме сторон AB
и AC
. (Формула Архимеда.)
Указание. Отложите на луче AC
отрезок AP
равный AB
. Докажите, что треугольник CKP
— равнобедренный.
Решение. Первый способ. Пусть AC\geqslant AB
, F
— проекция точки K
на прямую AB
. Отложим на луче AC
отрезок AP
, равный AB
. Пусть K_{1}
— проекция точки K
на AC
. Поскольку \angle CAK=\angle KAB
и треугольники APK
и ABK
равны (по двум сторонам и углу между ними), то PK=KB=KC
. Поэтому K_{1}
— середина PC
.
Из равенства треугольников AK_{1}K
и AFK
следует, что AK_{1}=AF
. Но
AK_{1}=\frac{AC+AP}{2}=\frac{AC+AB}{2}.
Второй способ. Пусть K_{1}
— проекция точки K
на AC
, R
— радиус окружности,
\angle ACK=\alpha,~\angle BCK=\angle CBK=\angle CAK=BAK=\beta.
По теореме синусов (см. задачу 23)
AB=2R\sin\angle ACB=2R\sin(\alpha-\beta),~AK=2R\sin\angle ACK=2R\sin\alpha,
AC=2R\sin\angle AKC=2R\sin(180^{\circ}-\alpha-\beta)=2R\sin(\alpha+\beta),
а так как
AK_{1}=AK\cos\beta=2R\sin\alpha\cos\beta,
то
AK_{1}=\frac{AB+AC}{2}~\Leftrightarrow~2R\sin\alpha\cos\beta=\frac{2R\sin(\alpha-\beta)+2R\sin(\alpha+\beta)}{2}~\Leftrightarrow
\Leftrightarrow~\sin\alpha\cos\beta=\frac{1}{2}(\sin(\alpha-\beta)+\sin(\alpha+\beta)).
Последнее равенство есть известная формула тригонометрии.
Примечание. См. также статью А.Спивака «Биссектриса и сумма синусов», Квант, 2011, N4, с.27 и 46.
Автор: Мазов Р. А.
Источник: Журнал «Квант». — 1982, № 3, с. 28, М734; 1982, № 9, с. 40, М734
Источник: Задачник «Кванта». — М734
Источник: Всесибирская физико-математическая олимпиада. — 2010, заключительный этап, задача 5, 10 класс
