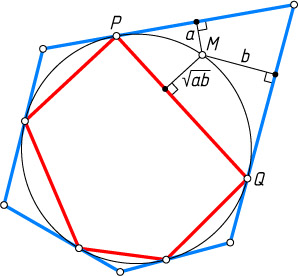
182. Около окружности описан многоугольник. Точки касания его сторон с окружностью служат вершинами второго, вписанного в эту окружность многоугольника. Докажите, что произведение расстояний от произвольной точки M
окружности до сторон (или их продолжений) одного многоугольника равно произведению расстояний от этой точки до сторон (или их продолжений) второго.
Указание. Расстояние от точки M
, лежащей на окружности, до хорды есть среднее геометрическое расстояний от этой точки до касательных, проведённых через концы хорды.
Решение. Пусть точка M
лежит на любой из двух дуг PQ
. Тогда расстояние от неё до хорды PQ
есть среднее геометрическое расстояний от этой точки до касательных к окружности, проведённых в точках P
и Q
(см. задачу 120).
Применим это утверждение к каждой стороне вписанного многоугольника и перемножим почленно полученные равенства.
Источник: Моденов П. С. Сборник задач по специальному курсу элементарной математики. — М.: Советская наука, 1957. — № 49, с. 199
Источник: Журнал «Квант». — 1974, № 12, с. 46, М256
Источник: Задачник «Кванта». — М256
