183. С помощью циркуля и линейки постройте треугольник по центрам описанной, вписанной и одной из вневписанных окружностей.
Указание. Описанная окружность делит пополам отрезок, соединяющий центры вписанной и вневписанной окружностей.
Решение. Пусть O
, O_{1}
, O_{2}
— данные центры в указанном порядке. Построим на отрезке O_{1}O_{2}
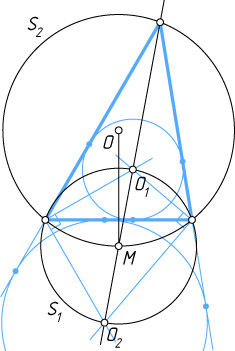
как на диаметре окружность. Тогда две вершины треугольника лежат на этой окружности, а её центр лежит на описанной окружности и на биссектрисе третьего угла (см. задачу 57).
Отсюда вытекает следующий способ построения. Строим на отрезке O_{1}O_{2}
как на диаметре окружность S_{1}
. Пусть M
— середина O_{1}O_{2}
, т. е. центр этой окружности. Радиусом OM
строим окружность S_{2}
с центром O
.
Пересечение окружностей S_{1}
и S_{2}
даёт две вершины искомого треугольника, а пересечение прямой O_{1}O_{2}
с окружностью S_{2}
— третью вершину.
Автор: Мартынов Б. В.
Источник: Журнал «Квант». — 1974, № 3, с. 34, М253
Источник: Задачник «Кванта». — М253
Источник: Куланин Е. Д., Федин С. Н. Геометрия треугольника в задачах: Экспериментальное учебное пособие для 8—10 кл. школ физико-математического направления. — М.: НИИ школ, 1990. — № 6(а), с. 55
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 8.35, с. 199
