243. Три равных окружности S_{1}
, S_{2}
, S_{3}
попарно касаются друг друга, и вокруг них описана окружность S
, которая касается всех трёх. Докажите, что для любой точки M
окружности S
касательная, проведённая из точки M
к одной из трёх окружностей S_{1}
, S_{2}
, S_{3}
, равна сумме касательных, проведённых из точки M
к двум другим окружностям.
Указание. Примените теорему косинусов.
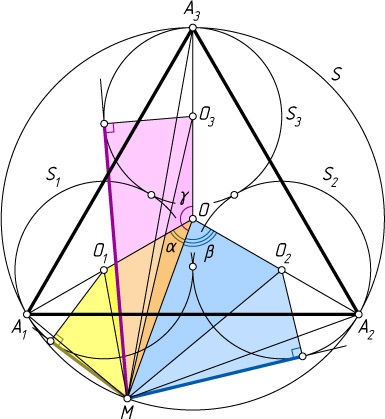
Решение. Пусть O_{1}
, O_{2}
, O_{3}
, O
— центры окружностей S_{1}
, S_{2}
, S_{3}
, S
соответственно; A_{1}
, A_{2}
, A_{3}
— точки касания окружностей S_{1}
, S_{2}
, S_{3}
с окружностью S
.
Предположим, что точка M
лежит на дуге A_{1}A_{2}
, не содержащей точки A_{3}
. Обозначим через \alpha
, \beta
, \gamma
углы между лучом OM
и лучами OO_{1}
, OO_{2}
, OO_{3}
соответственно. Тогда, если r
— радиус каждой из трёх меньших окружностей, а R
— радиус большей, то по теореме косинусов
MO_{1}^{2}=R^{2}+(R-r)^{2}-2R(R-r)\cos\alpha,
MO_{2}^{2}=R^{2}+(R-r)^{2}-2R(R-r)\cos\beta,
MO_{3}^{2}=R^{2}+(R-r)^{2}-2R(R-r)\cos\gamma.
Тогда квадраты касательных, проведённых из точки M
к окружностям S_{1}
, S_{2}
, S_{3}
, соответственно равны:
MO_{1}^{2}-r^{2}=2R(R-r)(1-\cos\alpha)=4R(R-r)\sin^{2}\frac{\alpha}{2},
MO_{2}^{2}-r^{2}=2R(R-r)(1-\cos\beta)=4R(R-r)\sin^{2}\frac{\beta}{2},
MO_{3}^{2}-r^{2}=2R(R-r)(1-\cos\gamma)=4R(R-r)\sin^{2}\frac{\gamma}{2}.
Поэтому касательные равны
2\sqrt{R(R-r)}\sin\frac{\alpha}{2},~2\sqrt{R(R-r)}\sin\frac{\beta}{2},~2\sqrt{R(R-r)}\sin\frac{\gamma}{2}
(синусы неотрицательны, так как
0\leqslant\frac{\alpha}{2}\leqslant180^{\circ},~0\leqslant\frac{\beta}{2}\leqslant180^{\circ},~0\leqslant\frac{\gamma}{2}\leqslant180^{\circ}).
Осталось проверить равенство
\sin\frac{\gamma}{2}=\sin\frac{\alpha}{2}+\sin\frac{\beta}{2}.
Действительно, рассмотрим равносторонний треугольник A_{1}A_{2}A_{2}
. Точка M
лежит на его описанной окружности, поэтому MA_{1}+MA_{2}=MA_{3}
(см. задачу 17), а так как
MA_{1}=2R\sin\frac{\alpha}{2},~MA_{2}=2R\sin\frac{\beta}{2},~MA_{3}=2R\sin\frac{\gamma}{2},
то
2R\sin\frac{\alpha}{2}+2R\sin\frac{\beta}{2}=2R\sin\frac{\gamma}{2}.
Следовательно,
\sin\frac{\gamma}{2}=\sin\frac{\alpha}{2}+\sin\frac{\beta}{2}.
Что и требовалось доказать.
Примечание. Утверждение останется верным, если в качестве S_{1}
, S_{2}
, S_{3}
взять любые равные окружности с центрами в вершинах правильного треугольника.
Источник: Журнал «Квант». — 1970, № 4, с. 27, М18(а)
Источник: Задачник «Кванта». — М18(а)
