244. Через точку касания двух окружностей проведена секущая. Докажите, что радиусы и касательные, проведённые через концы образовавшихся хорд, параллельны.
Указание. Докажите равенство углов, образованных соответствующими радиусами с секущей. Не забудьте рассмотреть оба возможных случая: внешнего и внутреннего касания окружностей. (Или примените гомотетию.)
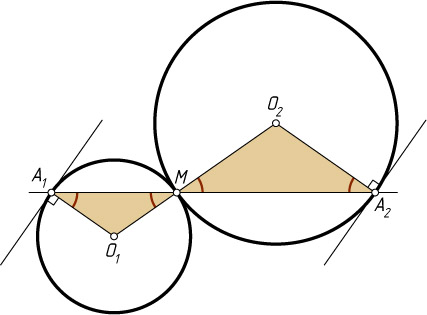
Решение. Первый способ. Рассмотрим случай внешнего касания. Пусть O_{1}
и O_{2}
— центры окружностей, M
— точка касания, A_{1}
и A_{2}
— соответственно точки пересечения окружностей с секущей. Тогда
\angle O_{1}A_{1}M=\angle O_{1}MA_{1}=\angle O_{2}MA_{2}=\angle O_{2}A_{2}M.
Поскольку накрест лежащие углы равны, то прямые O_{1}A_{1}
и O_{2}A_{2}
параллельны. Следовательно, параллельны и перпендикулярные им касательные.
Аналогично для случая внутреннего касания окружностей.
Второй способ. При гомотетии с центром в точке касания и коэффициентом, равным по модулю отношению радиусов окружностей, одна окружность переходит в другую (см. задачу 6401). При этом точка A_{1}
переходит в A_{2}
, касательная к первой окружности, проведённая в точке A_{1}
, — в параллельную ей касательную к второй окружности, проведённую в точке A_{2}
, а радиус O_{1}A_{1}
— в параллельный ему радиус O_{2}A_{2}
.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 33, с. 37
