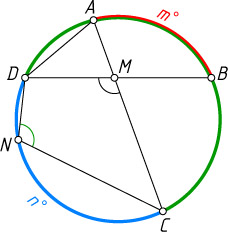
253. Из концов дуги AB
, содержащей m^{\circ}
, проведены хорды AC
и BD
, так, что угол DMC
, образованный их пересечением, равен углу DNC
, вписанному в дугу CD
. Найдите градусную меру этой дуги.
Ответ. 180^{\circ}-\frac{m^{\circ}}{2}
.
Указание. \angle DMC=\frac{\cup AB+\cup DNC}{2}
.
Решение. Обозначим градусную меру дуги DNC
через n^{\circ}
. Тогда
\angle DNC=\frac{\cup DAC}{2}=\frac{360^{\circ}-n^{\circ}}{2}=180^{\circ}-\frac{n^{\circ}}{2}.
Поскольку \angle DMC=\frac{\cup AB+\cup DNC}{2}
(см. задачу 26), то
180^{\circ}-\frac{n^{\circ}}{2}=\frac{m^{\circ}+n^{\circ}}{2}.
Отсюда находим, что n^{\circ}=180^{\circ}-\frac{m^{\circ}}{2}
.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 42, с. 38
