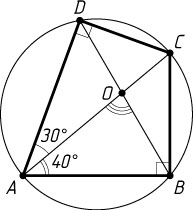
254. В четырёхугольнике ABCD
углы B
и D
— прямые. Диагональ AC
образует со стороной AB
острый угол в 40^{\circ}
, а со стороной AD
— угол в 30^{\circ}
. Найдите острый угол между диагоналями AC
и BD
.
Ответ. 80^{\circ}
.
Указание. Угол между пересекающимися хордами равен полусумме противоположных дуг, высекаемых на окружности этими хордами.
Решение. Точки A
, B
, C
и D
лежат на окружности с диаметром AC
. Поэтому
\cup AB=2\angle ACB=2(90^{\circ}-\angle CAB)=2(90^{\circ}-40^{\circ})=100^{\circ},
\cup DC=2\angle DAC=60^{\circ}.
Если O
— точка пересечения диагоналей, то
\angle AOB=\frac{\cup AB+\cup DC}{2}=\frac{160^{\circ}}{2}=80^{\circ}
(см. задачу 26).
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 43, с. 38
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 13.24, с. 105
