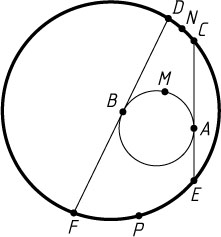
270. Внутри данной окружности находится другая окружность (см.рис.); CAE
и DBF
— две хорды большей окружности (не пересекающиеся), касающиеся меньшей окружности в точках A
и B
; CND
, EPF
— дуги между концами хорд. Найдите угловую величину дуги CND
, если дуги AMB
и EPF
содержат соответственно 154^{\circ}
и 70^{\circ}
.
Ответ. 18^{\circ}
.
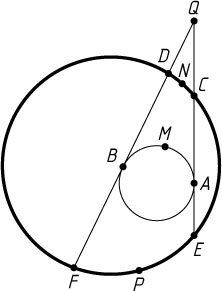
Указание. Если продолжения хорд пересекаются вне круга, то угол между ними равен полуразности угловых величин высекаемых ими дуг.
Решение. Пусть Q
— точка пересечения продолжений данных хорд. Тогда
\angle EQF=180^{\circ}-154^{\circ}=26^{\circ}.
Поскольку
\angle EQF=\frac{\smile EPF-\smile CND}{2}
(см. задачу 27), то
26^{\circ}=\frac{70^{\circ}-\smile CND}{2}.
Отсюда находим, что \smile CND=18^{\circ}
.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 51, с. 38

