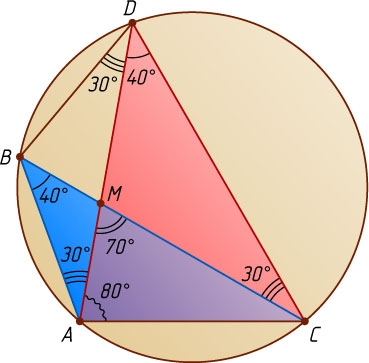
276. Треугольники ABC
и ADC
имеют общую сторону AC
; стороны AD
и BC
пересекаются в точке M
. Углы B
и D
равны по 40^{\circ}
. Расстояние между вершинами D
и B
равно стороне AB
, \angle AMC=70^{\circ}
. Найдите углы треугольников ABC
и ADC
.
Ответ. \angle BAC=110^{\circ}
, \angle BCA=30^{\circ}
, \angle DCA=60^{\circ}
, \angle DAC=80^{\circ}
.
Указание. Точки A
, B
, C
, D
лежат на одной окружности.
Решение. Точки A
, B
, C
, D
лежат на одной окружности (см. задачу 12); \angle AMC
— внешний угол треугольника DMC
. Поэтому \angle DCM=30^{\circ}
. Тогда
\angle BCA=\angle ADB=\angle BAD=\angle BCD=\angle DCM=30^{\circ}.
Следовательно,
\angle DCA=60^{\circ},~\angle BAC=110^{\circ},~\angle DAC=80^{\circ}.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 57, с. 39
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 13.15, с. 104
