280. С помощью циркуля и линейки постройте параллелограмм по его углу и диагоналям.
Указание. Задача сводится к построению треугольника по основанию, углу и медиане, проведённой к основанию.
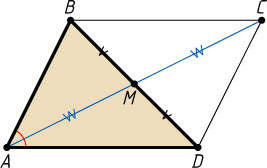
Решение. Построим треугольник по основанию, равному одной из диагоналей, углу при противоположной вершине, равному данному углу параллелограмма, и медиане, проведённой к основанию, равной половине второй диагонали параллелограмма (см. задачу 278). Достроим полученный треугольник до параллелограмма, продолжив его медиану на её же длину вне треугольника.

Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 62, с. 40
Источник: Делоне Б. Н., Житомирский О. К. Задачник по геометрии. — М.—Л.: ОГИЗ, 1949. — № 135, с. 15