278. С помощью циркуля и линейки постройте треугольник по основанию, углу при вершине и медиане, проведённой к основанию.
Указание. Геометрическое место точек, из которых данный отрезок виден под данным углом, есть две дуги равных окружностей (см. задачи 12 и 2889).
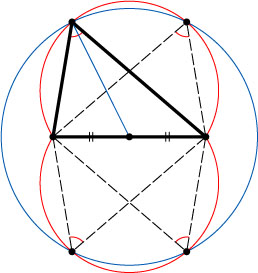
Решение. Построим две дуги равных окружностей так, чтобы из каждой точки этих дуг основание треугольника было видно под данным углом (см. задачу 2889).
С центром в середине данного основания проведём окружность радиусом, равным медиане. Каждая точка пересечения этой окружности с построенными дугами есть вершина искомого треугольника.

Источник: Петерсен Ю. Методы и теории для решения геометрических задач на построение, приложенные более чем к 400 задачам. — М.: Типография Э. Лисснера и Ю. Романа, 1892. — № 18, с. 12
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 58, с. 40
Источник: Пойа Д. Математическое открытие. — М.: Наука, 1970. — № 11, с. 39
Источник: Голубев В. И., Ерганжиева Л. Н., Мосевич К. К. Построение треугольника. — М.: БИНОМ. Лаборатория Знаний, 2008. — № 14, с. 55