289. Радиус окружности, вписанной в прямоугольный треугольник, равен r
, а половина периметра равна p
. Найдите гипотенузу.
Ответ. p-r
.
Указание. См. задачу 219.
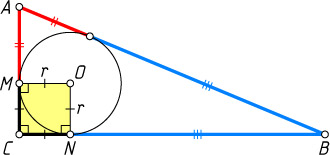
Решение. Вершина C
прямого угла данного треугольника, центр O
вписанной окружности и точки касания M
и N
с катетами являются вершинами квадрата со стороной r
. Значит, CM=ON=r
. Из равенства r=CM=p-c
(см. задачу 219) находим, что c=p-r
.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 71, с. 40
