314. Дана прямоугольная трапеция. Окружность, построенная на меньшей боковой стороне как на диаметре, касается другой боковой стороны и делит её на отрезки, равные a
и b
. Найдите радиус окружности.
Ответ. \sqrt{ab}
.
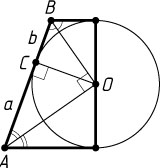
Указание. Отрезки, соединяющие центр окружности с концами большей боковой стороны трапеции, взаимно перпендикулярны.
Решение. Радиус, проведённый из центра O
окружности в точку C
касания окружности с боковой стороной AB
, есть высота прямоугольного треугольника AOB
, опущенная из вершины прямого угла на гипотенузу (см. задачу 313). Следовательно,
OC^{2}=AC\cdot CB=ab.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 4.14, с. 30
