315. В прямоугольную трапецию вписана окружность радиуса R
. Найдите стороны трапеции, если её меньшее основание равно \frac{4}{3}R
.
Ответ. \frac{10}{3}R
, 4R
, 2R
.
Указание. Проведите радиус в точку касания с большей боковой стороной трапеции и примените теорему о высоте, опущенной из вершины прямого угла на гипотенузу.
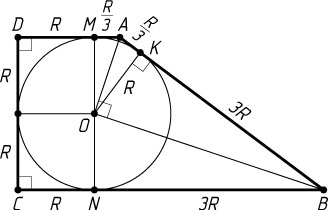
Решение. Пусть K
— точка касания вписанной окружности (с центром O
) с большей боковой стороной AB
трапеции ABCD
, M
и N
— точки касания с меньшим и большим основаниями AD
и BC
соответственно. Тогда
AK=AM=\frac{4}{3}R-R=\frac{1}{3}R,
а так как треугольник AOB
прямоугольный (см. задачу 313) и OK
— его высота, опущенная на гипотенузу, то AK\cdot BK=OK^{2}
, или BK\cdot\frac{1}{3}R=R^{2}
. Отсюда находим, что
BK=3R,~BC=CN+NB=R+3R=4R,~AB=\frac{1}{3}R+3R=\frac{10}{3}R.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.231, с. 174
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 4.15, с. 31
