318. В равнобедренную трапецию, периметр которой равен 8, а площадь 2, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.
Ответ. \frac{2-\sqrt{3}}{4}
.
Указание. Найдите радиус вписанной окружности, отрезки, на которые точка касания делит боковую сторону, и тангенс угла между диагональю и основанием трапеции.
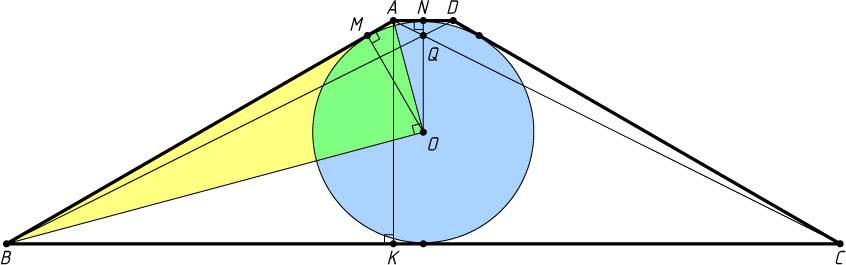
Решение. Пусть AD
— меньшее основание, AB
— боковая сторона, BC
— большее основание трапеции ABCD
, M
— точка касания окружности со стороной AB
, N
— со стороной AD
, Q
— точка пересечения диагоналей, O
— центр окружности, R
— её радиус.
Поскольку трапеция описана около окружности, сумма её боковых сторон равна сумме оснований, т. е. 4, поэтому
S_{ABCD}=2R\cdot\frac{AD+BC}{2}=2R\cdot\frac{4}{2}=4R.
Значит, R=\frac{1}{2}
.
С другой стороны, треугольник AOB
прямоугольный (см. задачу 313), а OM
— его высота, опущенная на гипотенузу, поэтому
AM\cdot MB=OM^{2}=R^{2},~\mbox{или}~AM(AB-AM)=R^{2},~\mbox{или}~AM(2-AM)=\frac{1}{4}.
Из этого уравнения находим, что AM=\frac{2-\sqrt{3}}{2}
.
Пусть K
— основание высоты AK
трапеции ABCD
. Тогда
CK=\frac{AD+BC}{2}=2,~\tg\angle NAQ=\tg\angle ACK=\frac{AK}{CK}=\frac{1}{2},
QN=NA\tg\angle NAQ=MA\tg\angle NAQ=\frac{2-\sqrt{3}}{4}.
