323. Стороны треугольника относятся как 5:4:3
. Найдите отношения отрезков сторон, на которые они делятся точками касания с вписанной окружностью.
Ответ. 3:1
, 3:2
, 2:1
.
Указание. Данный треугольник — прямоугольный.
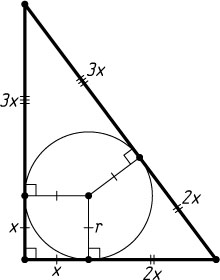
Решение. Данный треугольник — прямоугольный. Его катеты равны 3x
и 4x
, а гипотенуза равна 5x
. Если r
— радиус вписанной окружности, то
r=\frac{3x+4x-5x}{2}=x
(см. задачу 217). Четырёхугольник, вершины которого центр окружности, точки касания с катетами и вершина прямого угла треугольника, — квадрат. Следовательно, расстояния от вершин острых углов треугольника до точек касания равны 2x
и 3x
.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.252, с. 175
