329. В равнобедренную трапецию с основаниями a
и b
вписана окружность. Найдите диагональ трапеции.
Ответ. \frac{1}{2}\sqrt{a^{2}+6ab+b^{2}}
.
Указание. Диагональ данной трапеции — это гипотенуза прямоугольного треугольника, один катет которого — высота, проведённая из вершины верхнего основания, а второй — часть нижнего основания, равная средней линии трапеции. Высота трапеции равна диаметру вписанного круга.
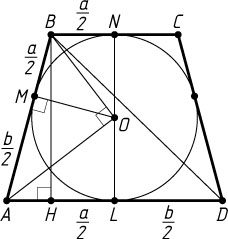
Решение. Пусть окружность с центром O
, вписанная в равнобедренную трапецию ABCD
, касается боковой стороны AB
в точке M
, а оснований BC
и AD
— в точках N
и L
соответственно.
Поскольку OM
— высота прямоугольного треугольника AOB
(см. задачу 656), опущенная из вершины прямого угла, то
OM=\sqrt{MA\cdot MB}=\sqrt{AL\cdot BN}=\sqrt{\frac{a}{2}\cdot\frac{b}{2}}=\frac{\sqrt{ab}}{2}.
Опустим перпендикуляр BH
на AD
. Тогда (см. задачу 1921)
DH=\frac{BC+AD}{2}=\frac{a+b}{2},~BH=2OM=\sqrt{ab}.
Из прямоугольного треугольника BHD
находим, что
BD=\sqrt{BH^{2}+DH^{2}}=\sqrt{ab+\left(\frac{a+b}{2}\right)^{2}}=\frac{1}{2}\sqrt{a^{2}+6ab+b^{2}}.
Источник: Пособие по математике для поступающих в вузы / Под ред. Г. Н. Яковлева. — 3-е изд. — М.: Наука, 1988. — № 27, с. 406
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 4.18, с. 31
