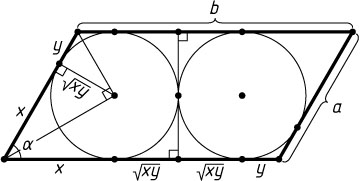
342. Прямая, перпендикулярная двум сторонам параллелограмма, делит его на две трапеции, в каждую из которых можно вписать окружность. Найдите острый угол параллелограмма, если его стороны равны a
и b
(a\lt b)
.
Ответ. \arcsin\left(\frac{b}{a}-1\right)
.
Указание. Полученные трапеции равны между собой. Пусть точка касания делит сторону, равную a
, на отрезки x
и y
. Тогда радиус каждой окружности равен \sqrt{xy}
(см. задачу 314).
Решение. Полученные трапеции равны между собой. Точка касания меньшей стороны параллелограмма делит эту сторону на отрезки с длинами x
и y
(x+y=a
). Тогда радиус окружности равен \sqrt{xy}
(см. задачу 656), высота параллелограмма равна 2\sqrt{xy}
, большая сторона равна b=y+2\sqrt{xy}+x
. Тогда 2\sqrt{xy}=b-x-y=b-a
, следовательно,
\sin\alpha=\frac{2\sqrt{xy}}{x+y}=\frac{b-a}{a},
где \alpha
— искомый угол.
Источник: Шарыгин И. Ф. Факультативный курс по математике. Решение задач: Учебное пособие для 10 кл. — М.: Просвещение, 1989. — № 93, с. 198
