347. В треугольнике ABC
с периметром 2p
острый угол ABC
равен \alpha
и AC=a
. В треугольник вписана окружность с центром в точке O
. Найдите площадь треугольника AOC
.
Ответ. \frac{1}{2}a(p-a)\tg\frac{\alpha}{2}
.
Указание. Расстояние от вершины треугольника до ближайшей точки касания с вписанной окружностью равно разности полупериметра и противолежащей стороны треугольника (см. задачу 219).
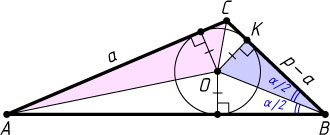
Решение. Пусть K
— точка касания вписанной окружности со стороной BC
. Тогда BK=p-a
(см. задачу 219) и
OK=BK\tg\frac{\alpha}{2}=(p-a)\tg\frac{\alpha}{2}.
Поскольку OK
— радиус вписанного круга, то
S_{\triangle AOC}=\frac{1}{2}a(p-a)\tg\frac{\alpha}{2}.
Источник: Вступительный экзамен на механико-математический факультет МГУ. — 1983, № 3, вариант 3
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — № 3, с. 15
