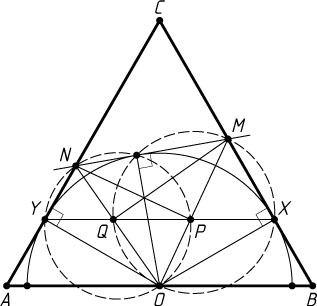
357. В равносторонний треугольник ABC
вписана полуокружность с центром O
на стороне AB
. Некоторая касательная к полуокружности пересекает стороны BC
и CA
в точках M
и N
соответственно, а прямая, соединяющая точки касания сторон BC
и AC
с полуокружностью, пересекает отрезки OM
и ON
в точках P
и Q
. Докажите, что MN=2PQ
.
Указание. Докажите, что MQ
и NP
— высоты треугольника NOM
.
Решение. Пусть X
и Y
— точки касания полуокружности со сторонами BC
и AC
. Тогда
\angle NOM=\frac{1}{2}\angle XOY=\frac{1}{2}(180^{\circ}-60^{\circ})=60^{\circ},~\angle CXY=60^{\circ}.
Поэтому точки M
, X
, O
и Q
лежат на одной окружности, причём MO
— диаметр этой окружности. Следовательно, MQ
— высота треугольника MON
. Аналогично докажем, что NP
— высота треугольника MON
. Поэтому треугольник POQ
подобен треугольнику NOM
с коэффициентом
\cos\angle NOM=\cos60^{\circ}=\frac{1}{2}
(см. задачу 19). Следовательно,
MN=\frac{PQ}{\cos60^{\circ}}=2PQ.
Источник: Куценок В. Е. Метод вспомогательной окружности: Рукопись. — Киев. — № 50, с. 15
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 803, с. 99
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 13.38, с. 106
