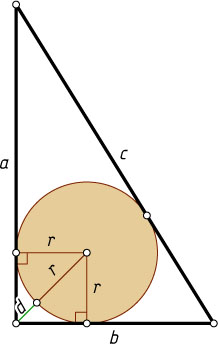
358. В прямоугольном треугольнике даны катеты a
и b
. Найдите расстояние от вершины прямого угла до ближайшей к ней точки вписанной окружности.
Ответ. \frac{(a+b-\sqrt{a^{2}+b^{2}})(\sqrt{2}-1)}{2}
.
Указание. Найдите радиус вписанного круга.
Решение. Найдём гипотенузу c
и радиус вписанного круга r
:
c=\sqrt{a^{2}+b^{2}},~r=\frac{a+b-c}{2}=\frac{a+b-\sqrt{a^{2}+b^{2}}}{2}
(см. задачу 217). Пусть d
— искомое расстояние. Тогда
d=r\sqrt{2}-r=r(\sqrt{2}-1)=\frac{(a+b-\sqrt{a^{2}+b^{2}})(\sqrt{2}-1)}{2}.
Источник: Шарыгин И. Ф. Факультативный курс по математике. Решение задач: Учебное пособие для 10 кл. — М.: Просвещение, 1989. — № 73, с. 197
