405. В равнобедренном треугольнике ABC
на основании AC
взята точка M
так, что AM=a
, MC=b
. В треугольники ABM
и CBM
вписаны окружности. Найдите расстояние между точками касания этих окружностей с отрезком BM
.
Ответ. \frac{|a-b|}{2}
.
Указание. Расстояние от вершины треугольника до ближайшей точки касания с вписанной окружностью равно разности между полупериметром и противолежащей стороной (задача 219).
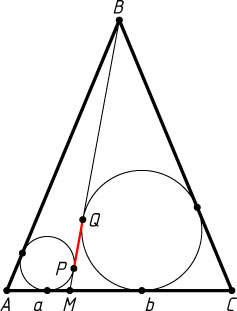
Решение. Пусть P
и Q
— точки касания окружностей, вписанных в треугольники ABM
и CBM
, со стороной BM
. Тогда искомое расстояние равно |BP-BQ|
.
Пусть p_{1}
и p_{2}
— полупериметры этих треугольников. Тогда BP=p_{1}-a
, BQ=p_{2}-b
(см. задачу 219). Следовательно,
|BP-BQ|=|p_{1}-a-p_{2}+b|=
=\left|b-a-\frac{b-a}{2}\right|=\frac{|a-b|}{2}.
Источник: Вступительный экзамен в МФТИ. — 1970, № 4, билет 12
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 70-4-12, с. 143
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 28, с. 9
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 28, с. 7
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 3.3, с. 56
