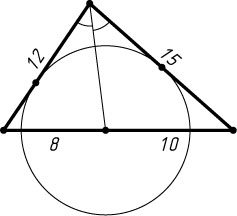
419. Дан треугольник со сторонами 12, 15, 18. Проведена окружность, касающаяся обеих меньших сторон и имеющая центр на большой стороне. Найдите отрезки, на которые центр окружности делит большую сторону треугольника.
Ответ. 8 и 10.
Указание. Центр окружности, вписанной в угол, лежит на биссектрисе этого угла.
Решение. Центр окружности лежит на биссектрисе большего угла. Поэтому отношение искомых отрезков равно отношению боковых сторон (см. задачу 1509), т. е. \frac{4}{5}
. Следовательно, искомые отрезки равны
\frac{4}{9}\cdot18=8,~\frac{5}{9}\cdot18=10.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.013, с. 159
