1509. Докажите, что биссектриса треугольника делит его сторону на отрезки, пропорциональные двум другим сторонам.
Указание. Через одну из вершин основания проведите прямую, параллельную противолежащей стороне треугольника, и продолжите биссектрису до пересечения с этой прямой.
Решение. Первый способ. Пусть CD
— биссектриса треугольника ABC
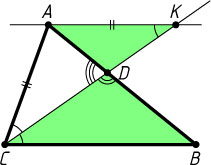
(рис. 1). Проведём через вершину A
прямую, параллельную BC
, и продолжим биссектрису до пересечения с этой прямой в точке K
. Поскольку \angle ACK=\angle KCB=\angle CKA
, то треугольник CAK
— равнобедренный, AK=AC
.
Из подобия треугольников ADK
и BDC
следует, что AK:BC=AD:DB
, а так как AK=AC
, то AC:BC=AD:DB
.
Второй способ. Пусть CD
— биссектриса треугольника ABC
(рис. 1). По теореме синусов из треугольников ACD
и BCD
находим, что
\frac{AD}{\sin\angle ACD}=\frac{AC}{\sin\angle ADC},~\frac{DB}{\sin\angle BCD}=\frac{BC}{\sin\angle BDC}.
Разделим почленно полученные равенства друг на друга. Поскольку
\sin\angle ACD=\sin\angle BCD,~\sin\angle ADC=\sin\angle BDC,
то \frac{AD}{DB}=\frac{AC}{CB}
.
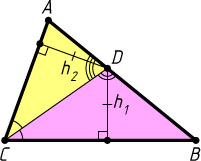
Третий способ. Пусть CD
— биссектриса треугольника ABC
(рис. 2). Обозначим через h_{1}
и h_{2}
— высоты треугольников ADC
и BDC
, проведённые из вершины D
. Тогда
S_{\triangle ADC}=\frac{1}{2}AC\cdot h_{1}=\frac{1}{2}AD\cdot DC\cdot\sin\angle ADC,
S_{\triangle BDC}=\frac{1}{2}BC\cdot h_{2}=\frac{1}{2}BD\cdot DC\cdot\sin\angle BDC.
Разделим почленно полученные равенства друг на друга. Поскольку
\sin\angle ADC=\sin\angle BDC,~h_{1}=h_{2},
то \frac{AD}{DB}=\frac{AC}{CB}
.
Примечание. 1. Аналогичное утверждение верно и для биссектрисы внешнего угла треугольника (см. задачу 1645).
2. Верно также и обратное утверждение: если точка D
, лежащая на прямой AB
, делит отрезок AB
(внутренним или внешним образом) на отрезки, пропорциональные сторонам AC
и BC
треугольника ABC
, то CD
— биссектриса внутреннего или внешнего угла треугольника ABC
(см. задачу 1510).
3. См. также статью С.Р.Сефибекова «Четыре доказательства теоремы о биссектрисах», Квант, 1983, N8, с.37.
4. См. также статью Б.Ивлева «Ещё 13 доказательств теоремы о биссектрисе», Квант, 1985, N2, с.29-30.
Источник: Адамар Ж. Элементарная геометрия. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1948. — с. 114
Источник: Шарыгин И. Ф. Геометрия 7—9: Учебник для общеобразовательных учебных заведений. — М.: Дрофа, 2002. — с. 267
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — с. 5
Источник: Куланин Е. Д., Федин С. Н. Геометрия треугольника в задачах: Экспериментальное учебное пособие для 8—10 кл. школ физико-математического направления. — М.: НИИ школ, 1990. — № 26, с. 99
Источник: Готман Э. Г., Скопец З. А. Решение геометрических задач аналитическим методом: Пособие для учащихся 9—10 кл. — М.: Просвещение, 1979. — № 165, с. 30
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 1.17(а), с. 13
Источник: Калинин А. Ю., Терёшин Д. А. Геометрия. 10—11 классы. — М.: МЦНМО, 2011. — с. 573

