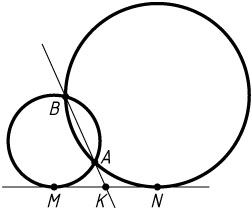
444. Докажите, что прямая, проходящая через точки пересечения двух окружностей, делит пополам общую касательную к ним.
Указание. Примените теорему о касательной и секущей.
Решение. Первый способ. Пусть A
и B
— точки пересечения двух окружностей, MN
— общая касательная (M
и N
— точки касания), K
— точка пересечения прямых AB
и MN
(A
между K
и B
). Тогда
MK^{2}=KB\cdot KA~\mbox{и}~NK^{2}=KB\cdot KA.
Следовательно, MK=NK
.
Второй способ. Прямая AB
— радикальная ось описанных окружностей треугольников ABM
и ABN
(см. задачу 6392). Следовательно, точка её пересечения с общей касательной MN
этих окружностей — середина отрезка MN
.
Примечание. Другая формулировка этой задачи: если точка B
, лежащая внутри треугольника MAN
, такова, что описанные окружности треугольников ABM
и ABN
касаются прямой MN
, то прямая AB
проходит через середину стороны MN
.
Такую точку иногда называют точкой Шалтая.
Источник: Яглом И. М. Геометрические преобразования. — Т. 2: Линейные и круговые преобразования. — М.: ГИТТЛ, 1956. — № 245, с. 230
Источник: Шарыгин И. Ф. Факультативный курс по математике. Решение задач: Учебное пособие для 10 кл. — М.: Просвещение, 1989. — № 187, с. 206
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 3.10, с. 59
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 3.11, с. 57
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — с. 92
