445. Сторона AB
прямоугольника ABCD
равна 12, а сторона стороны AD
равна 5. Диагонали прямоугольника пересекаются в точке E
. Найдите отношение расстояния от точки E
до центра окружности, вписанной в треугольник AED
, к расстоянию от точки E
до центра окружности, вписанной в треугольник DEC
.
Ответ. \frac{10}{3}
.
Указание. Расстояние от вершины треугольника до ближайшей точки касания с вписанной окружностью равно разности полупериметра и противолежащей стороны (см. задачу 219).
Решение. По теореме Пифагора находим, что AC=BD=13
. Из свойств прямоугольника следует, что DE=AE=CE=\frac{1}{2}AC=\frac{13}{2}
.
Пусть O_{1}
и O_{2}
— центры окружностей, вписанных в треугольники AED
и CED
соответственно, M
и N
— точки касания окружностей с отрезком DE
, P
и Q
— середины AD
и DC
соответственно. Треугольники AED
и CED
равнобедренные, поэтому окружности касаются сторон AD
и CD
в точках P
и Q
. Обозначим \angle NO_{2}E=\angle PED=\alpha
. Тогда
\sin\alpha=\frac{DP}{DE}=\frac{5}{13},~\cos\alpha=\frac{12}{13},~\tg\alpha=\frac{5}{12}.
Пусть p_{1}
и p_{2}
— полупериметры треугольников AED
и CED
. Тогда
EM=p_{1}-AD=\frac{13}{2}+\frac{5}{2}-5=4,~EN=p_{2}-CD=\frac{13}{2}+6-12=\frac{1}{2}
(см. задачу 219),
EO_{1}=\frac{EM}{\cos\alpha},~EO_{2}=\frac{EN}{\sin\alpha}.
Следовательно,
\frac{EO_{1}}{EO_{2}}=\frac{\frac{EM}{\cos\alpha}}{\frac{EN}{\sin\alpha}}=\frac{EM}{EN}\cdot\tg\alpha=8\cdot\frac{5}{12}=\frac{10}{3}.
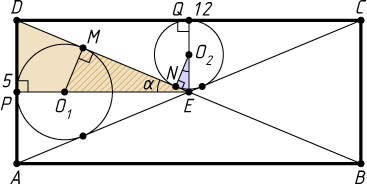
Источник: Вступительный экзамен на факультет почвоведения МГУ. — 1989, вариант 2, № 4
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Факториал, 1995. — с. 94
