452. Докажите, что площадь треугольника равна его полупериметру, умноженному на радиус вписанной окружности.
Указание. Соедините центр вписанной окружности с вершинами треугольника и сложите площади полученных треугольников.
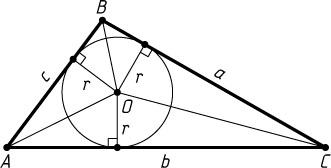
Решение. Первый способ. Соединим центр O
вписанной окружности радиуса r
треугольника ABC
с вершинами треугольника. Пусть BC=a
, AC=b
, AB=c
. Тогда
S_{\triangle ABC}=S_{\triangle BOC}+S_{\triangle AOC}+S_{\triangle AOB}=
=\frac{1}{2}ar+\frac{1}{2}br+\frac{1}{2}cr=\frac{a+b+c}{2}r=pr,
где p
— полупериметр треугольника.
Второй способ. На продолжениях стороны BC
за точки B
и C
отложим отрезки соответственно BP=AB
и CQ=AC
. По теореме о внешнем угле треугольника углы при основании AP
равнобедренного треугольника ABP
равны половине угла B
треугольника ABC
, т. е. углу OBA
. Значит, BO\parallel AP
. Аналогично, CO\parallel AQ
, поэтому треугольник BOC
подобен треугольнику PAQ
. Кроме того,
PQ=PB+BC+CQ=AB+BC+AC=2p,
где p
— полупериметр треугольника ABC
.
Пусть AH
— высота треугольника PAQ
, AF=r
— высота треугольника BOC
. Тогда из подобия \frac{OF}{AH}=\frac{BC}{PQ}
, или BC\cdot AH=OF\cdot PQ
. Следовательно,
S_{\triangle ABC}=\frac{1}{2}BC\cdot AH=\frac{1}{2}OF\cdot PQ=\frac{1}{2}r\cdot2p=rp.
Что и требовалось доказать
Примечание. Аналогичная формула верна для площади любого описанного многоугольника (см. задачу 523).
Источник: Адамар Ж. Элементарная геометрия. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1948. — № 299, с. 233
Источник: Пржевальский Е. Собрание геометрических теорем и задач. — М.: Типография Г. Лисснера и Д. Собко, 1909. — № 86, с. 144
Источник: Кокстер Г. С. М. Введение в геометрию. — М.: Наука, 1966. — № 1.52, с. 27-28
Источник: Погорелов А. В. Геометрия: Учебное пособие для 7—11 кл. средней школы. — 8-е изд. — М.: Просвещение, 1989. — № 36, с. 78
Источник: Шарыгин И. Ф. Геометрия 7—9: Учебник для общеобразовательных учебных заведений. — М.: Дрофа, 2002. — с. 256
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — с. 81
Источник: Кушнир И. А. Геометрия. Поиск и вдохновение. — М.: МЦНМО, 2013. — с. 512, формула 2
