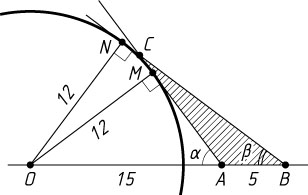
461. На прямой, проходящей через центр O
окружности радиуса 12, взяты точки A
и B
, причём OA=15
, AB=5
и A
лежит между O
и B
. Из точек A
и B
проведены касательные к окружности, точки касания которых лежат по одну сторону от прямой OB
. Найдите площадь треугольника ABC
, где C
— точка пересечения этих касательных.
Ответ. \frac{150}{7}
.
Указание. Примените теорему синусов к треугольнику ABC
.
Решение. Первый способ. Пусть касательные, проведённые из точек A
и B
касаются окружности в точках M
и N
соответственно. Обозначим CM=CN=x
. Из прямоугольных треугольников AMO
и BNO
находим, что
AM=\sqrt{AO^{2}-OM^{2}}=\sqrt{15^{2}-12^{2}}=9,
BN=\sqrt{BO^{2}-ON^{2}}=\sqrt{20^{2}-12^{2}}=16,
значит,
AC=AM+MC=9+x,~BC=BN-NC=16-x.
Центр окружности, вписанной в угол, лежит на биссектрисе этого угла, поэтому CO
— биссектриса внешнего угла при вершине C
треугольника ABC
. Тогда (см. задачу 1645)
\frac{AC}{CB}=\frac{AO}{OB},~\mbox{или}~\frac{9+x}{16-x}=\frac{15}{20},
откуда
x=\frac{12}{7},~BC=16-x=16-\frac{12}{7}=\frac{100}{7}.
Из прямоугольного треугольника BNO
находим, что
\sin\angle ABC=\sin\angle OBN=\frac{ON}{OB}=\frac{12}{20}=\frac{3}{5}.
Следовательно,
S_{\triangle ABC}=\frac{1}{2}AB\cdot BC\sin\angle ABC=\frac{1}{2}\cdot5\cdot\frac{100}{7}\cdot\frac{3}{5}=\frac{150}{7}.
Второй способ. Обозначим через M
и N
точки касания окружности с прямыми, проходящими через точки A
и B
соответственно, \angle OAM=\alpha
, \angle OBN=\beta
. Тогда
\angle ACB=\alpha-\beta,~\frac{OM}{OA}=\sin\alpha,~\frac{ON}{OB}=\sin\beta.
Поэтому
\sin\alpha=\frac{4}{5},~\sin\beta=\frac{3}{5},~\cos\alpha=\frac{3}{5},~\cos\beta=\frac{4}{5}.
По теореме синусов
\frac{BC}{AB}=\frac{\sin(180^{\circ}-\alpha)}{\sin(\alpha-\beta)},~BC=\frac{AB\sin\alpha}{\sin(\alpha-\beta)}=\frac{AB\sin\alpha}{\sin\alpha\cos\beta-\cos\alpha\sin\beta}=\frac{5\cdot\frac{4}{5}}{\frac{4}{5}\cdot\frac{4}{5}-\frac{3}{5}\cdot\frac{3}{5}}=\frac{100}{7}.
Следовательно,
S_{\triangle ABC}=\frac{1}{2}AB\cdot BC\sin\angle ABC=\frac{1}{2}\cdot5\cdot\frac{100}{7}\cdot\frac{3}{5}=\frac{150}{7}.
Источник: Вступительный экзамен на геологический факультет МГУ. — 1966, вариант 3, № 4
Источник: Моденов П. С. Экзаменационные задачи по математике с анализом их решения. — М.: Просвещение, 1969. — вариант 3, № 4, с. 47
Источник: Шарыгин И. Ф. Факультативный курс по математике. Решение задач: Учебное пособие для 10 кл. — М.: Просвещение, 1989. — № 164, с. 204
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 121, с. 15
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 8.26, с. 62
