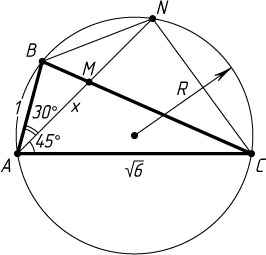
492. В треугольнике ABC
известно, что \angle BAC=75^{\circ}
, AB=1
, AC=\sqrt{6}
. На стороне BC
выбрана точка M
, причём \angle BAM=30^{\circ}
. Прямая AM
пересекает окружность, описанную около треугольника ABC
, в точке N
, отличной от A
. Найдите AN
.
Ответ. 2.
Указание. Обозначьте AN
через x
, выразите BN
и CN
через радиус описанной окружности треугольника ABC
и примените теорему косинусов к треугольникам ABN
и ACN
(или воспользуйтесь теоремой Птолемея).
Решение. Первый способ. Пусть AN=x
, R
— радиус описанной окружности треугольника. Тогда
BN=2R\sin30^{\circ}=R,~CN=2R\sin45^{\circ}=R\sqrt{2}.
По теореме косинусов из треугольников ABN
и ACN
находим, что
BN^{2}=R^{2}=AB^{2}+AN^{2}-2AB\cdot AN\cos30^{\circ}=1+x^{2}-x\sqrt{3},
CN^{2}=2R^{2}=6+x^{2}-2\sqrt{6}x\cdot\frac{1}{\sqrt{2}}=6+x^{2}-2x\sqrt{3}.
Из полученной системы уравнений находим, что x^{2}=4
. Следовательно, AN=x=2
.
Второй способ. Пусть R
— радиус окружности. Во вписанном четырёхугольнике ABNC
имеем:
BN=2R\sin30^{\circ}=R,~CN=2R\sin45^{\circ}=R\sqrt{2},~BC=2R\sin75^{\circ}.
По теореме Птолемея (см. задачу 130)
AB\cdot CN+AC\cdot BN=AN\cdot BC,~\mbox{или}~R\sqrt{2}+R\sqrt{6}=AN\cdot2R\sin75^{\circ}.
Следовательно,
AN=\frac{\sqrt{2}+\sqrt{6}}{2\sin75^{\circ}}=\frac{\sqrt{2}+\sqrt{6}}{2\cdot\frac{\sqrt{2}+\sqrt{6}}{4}}=2.
Источник: Вступительный экзамен на факультет почвоведения МГУ. — 1984, вариант 1, № 4
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — № 4, с. 506
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Факториал, 1995. — с. 83
