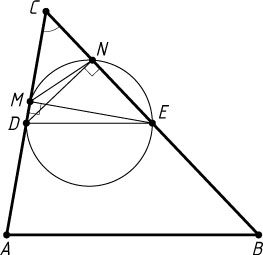
496. В треугольнике ABC
на средней линии DE
, параллельной AB
, как на диаметре построена окружность, пересекающая стороны AC
и BC
в точках M
и N
. Найдите MN
, если BC=a
, AC=b
, AB=c
.
Ответ. \frac{c(a^{2}+b^{2}-c^{2})}{4ab}
.
Указание. Треугольники CMN
и CED
подобны с коэффициентом |\cos\angle ACB|
(см. задачу 19).
Решение. Точки M
и N
лежат на окружности с диаметром DE
, поэтому DN
и EM
— высоты треугольника CDE
, значит, треугольники CMN
и CED
подобны с коэффициентом \cos\angle ACB
(см. задачу 19). Следовательно,
MN=DE\cos\angle ACB=\frac{c}{2}\cdot\frac{a^{2}+b^{2}-c^{2}}{2ab}=\frac{c(a^{2}+b^{2}-c^{2})}{4ab}.
Источник: Вступительный экзамен в МФТИ. — 1973, билет 7, № 3
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 73-7-3, с. 163
Источник: Шарыгин И. Ф. Факультативный курс по математике. Решение задач: Учебное пособие для 10 кл. — М.: Просвещение, 1989. — № 256, с. 212
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 174, с. 20
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 15.5, с. 122
