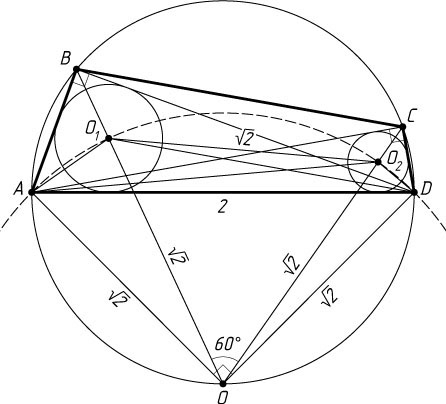
505. В выпуклом четырёхугольнике ABCD
проведены диагонали AC
и BD
. Известно, что AD=2
, \angle ABD=\angle ACD=90^{\circ}
, и расстояние между центрами окружностей, вписанных в треугольники ABD
и ACD
, равно \sqrt{2}
. Найдите BC
.
Ответ. \sqrt{3}
.
Указание. Точки A
, D
и центры указанных окружностей лежат на окружности, центр которой расположен на описанной окружности четырёхугольника ABCD
.
Решение. Первый способ. Пусть O_{1}
и O_{2}
— центры указанных окружностей. Поскольку
\angle AO_{1}D=\angle AO_{2}D=90^{\circ}+\frac{1}{2}\angle ACD=90^{\circ}+45^{\circ}=135^{\circ}
(см. задачу 1101), точки A
, O_{1}
, O_{2}
и D
лежат на одной окружности. Пусть O
— центр этой окружности, R
— её радиус. Тогда центральный угол AOD
равен 360^{\circ}-2\angle AO_{1}D=360^{\circ}-270^{\circ}=90^{\circ}
, значит, точка O
(так же, как и точки B
и C
) лежит на окружности с диаметром AD
, т. е. на окружности, описанной около данного четырёхугольника.
Треугольник AOD
прямоугольный и равнобедренный, поэтому
R=OA=OD=\frac{AD}{\sqrt{2}}=\frac{2}{\sqrt{2}}=\sqrt{2},
Точка O
— середина дуги AD
, не содержащей точки B
, значит, CO
и BO
— биссектрисы углов ACD
и ABD
, поэтому BO_{1}O
— одна прямая и CO_{2}O
— одна прямая.
Треугольник OO_{1}O_{2}
— равносторонний (OO_{1}=OO_{2}=R=\sqrt{2}=O_{1}O_{2}
), поэтому \angle BOC=\angle O_{1}OO_{2}=60^{\circ}
. Следовательно, по теореме синусов
BC=AD\sin60^{\circ}=2\cdot\frac{\sqrt{3}}{2}=\sqrt{3}.
Второй способ. Пусть O_{1}
и O_{2}
— центры указанных окружностей. Поскольку \angle ABD=\angle ACD=90^{\circ}
, точки B
и C
лежат на окружности с диаметром AD=2
. Продолжения биссектрис BO_{1}
и CO_{2}
треугольников ABD
и ACD
пересекают эту окружность в середине O
дуги AD
, не содержащей точки B
. Треугольник AOD
— прямоугольный и равнобедренный, поэтому OA=OD=\sqrt{2}
. Треугольник AOO_{1}
— равнобедренный, так как
\angle AO_{1}O=\angle ABO+\angle BAO=\frac{1}{2}\angle ABD+\frac{1}{2}\angle BAD,
\angle OAO_{1}=\angle OAD+\angle DAO_{1}=\angle OBD+\angle DAO_{1}=\frac{1}{2}\angle ABD+\frac{1}{2}\angle BAD=\angle AO_{1}O.
Тогда OA=OO_{1}
и OD=OO_{2}
, поэтому OO_{1}=OO_{2}=\sqrt{2}
. Треугольник OO_{1}O_{2}
— равносторонний, поэтому \angle BOC=\angle O_{1}OO_{2}=60^{\circ}
. Следовательно, по теореме синусов
BC=AD\sin60^{\circ}=2\cdot\frac{\sqrt{3}}{2}=\sqrt{3}.
Источник: Вступительный экзамен на географический факультет МГУ. — 1989, вариант 1, № 5
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Факториал, 1995. — с. 108
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 13.36, с. 106
