520. Из точки A
, расположенной вне окружности, проведены две касательные AM
и AN
(M
и N
— точки касания) и секущая, пересекающая окружность в точках P
и Q
. Пусть L
— середина PQ
. Докажите, что \angle MLA=\angle NLA
.
Указание. Если O
— центр данной окружности, точки O
, L
, M
, A
и N
лежат на одной окружности.
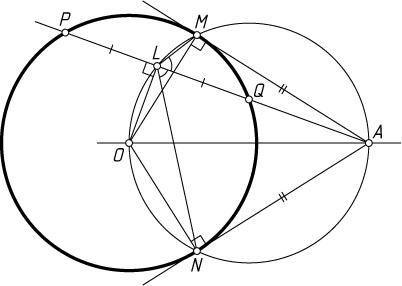
Решение. Пусть O
— центр окружности. Тогда OL\perp AL
. Отрезок OA
виден из точек L
, M
и N
под прямым углом. Поэтому точки O
, L
, M
, A
и N
лежат на одной окружности. Поскольку AM
и AN
— отрезки касательных, проведённых к окружности из одной точки, то AM=AN
. Следовательно,
\angle MLA=\angle NLA
(см. задачу 805).
Источник: Куценок В. Е. Метод вспомогательной окружности: Рукопись. — Киев. —
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 838, с. 103
