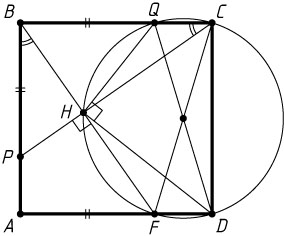
525. Дан квадрат ABCD
. Точки P
и Q
лежат на сторонах AB
и BC
соответственно, причём BP=BQ
. Пусть H
— основание перпендикуляра, опущенного из точки B
на отрезок PC
. Докажите, что угол DHQ
прямой.
Указание. Продолжите BH
до пересечения AD
в точке F
и опишите окружность около прямоугольника DFQC
.
Решение. Первый способ. Пусть F
— точка пересечения прямых AD
и BH
. Прямоугольные треугольники ABF
и BCP
равны по катету и прилежащему острому углу. Поэтому AF=BP=BQ
. Следовательно, QFDC
— прямоугольник.
Описанная около него окружность (FC
— её диаметр) проходит через точку H
(так как \angle CHF=90^{\circ}
), но DQ
— также диаметр этой окружности. Поэтому \angle DHQ=90^{\circ}
.
Второй способ. Обозначим \angle QBH=\alpha
(рис. 1). Отрезок BH
— высота, опущенная на гипотенузу прямоугольного треугольника PBC
, значит,
\angle DCH=\angle BPC=\angle QBH=\alpha,
\frac{BH}{BQ}=\frac{BH}{BP}=\cos(90^{\circ}-\alpha)=\sin\alpha=\frac{CH}{BC}=\frac{CH}{CD}.
Треугольники BQH
и CDH
подобны (по двум сторонам и углу между ними), следовательно, \angle QHB=\angle DHC
. Прибавив \angle CHQ
к обеим частям полученного равенства, получим, что
\angle DHQ=\angle BHC=90^{\circ}.
Третий способ. Пусть отрезки BD
и PQ
пересекаются в точке K
(рис. 2). Из равенства BP=BQ
следует, что \angle QKD=90^{\circ}=\angle QCD
. Значит, точки C
и K
лежат на окружности с диаметром QD
. Докажем, что точка H
лежит на той же окружности.
Пусть BD
и CP
пересекаются в точке S
. Тогда в треугольнике BSP
отрезки PK
и BH
являются высотами, следовательно, \angle SKH=\angle BPH
(см. задачу 141), а так как \angle BPH=\angle DCH
, то \angle DKH=\angle DCH
. Это и означает, что H
лежит на окружности с диаметром QD
(см. задачу 12). Следовательно, \angle DHQ=90^{\circ}
.
Четвёртый способ. Так как BH
— высота, проведённая к гипотенузе прямоугольного треугольника PBC
, то треугольники PBH
и BCH
подобны с коэффициентом
k=\frac{BP}{CB}=\frac{BH}{CH}=\frac{PH}{BH}.
Рассмотрим поворотную гомотетию \mathbf{H}_{H}^{k}\circ\mathbf{R}_{H}^{90^{\circ}}
. Образом точки C
при этом преобразовании является точка B
, а образом точки B
— точка P
. Образом любой прямой должна являться прямая, ей перпендикулярная, поэтому прямая CD
должна перейти в прямую BC
, а точка D
— в такую точку T
на отрезке BC
, что BT=k\cdot CD
. Поскольку
BQ=BP=k\cdot CB=k\cdot CD,
точка T
совпадёт с точкой Q
, т. е. Q
— образ точки D
при рассмотренной поворотной гомотетии. Поэтому \angle DHQ=90^{\circ}
.
Автор: Васильев Н. Б.
Источник: Московская математическая регата. — 2006-2007, 11 класс
Источник: Всесоюзная олимпиада по математике. — 1974, VIII, 10 класс
Источник: Журнал «Квант». — 1974, № 8, с. 44, М276
Источник: Задачник «Кванта». — М276
Источник: Васильев Н. Б., Егоров А. А. Задачи всесоюзных математических олимпиад. — М.: Наука, 1988. — № 195, с. 54
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 979, с. 120