534. В равнобедренном треугольнике высота равна 20, а основание относится к боковой стороне как 4:3
. Найдите радиус вписанной окружности.
Ответ. 8.
Указание. Найдите отношение, в котором биссектриса угла при основании делит высоту.
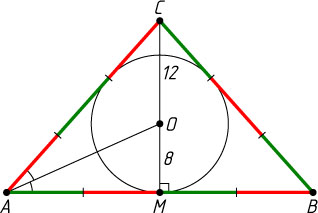
Решение. Пусть CM
— высота данного треугольника ABC
, CM=20
, AC=BC
, O
— центр вписанной окружности. Тогда OM
— радиус этой окружности.
Поскольку AO
— биссектриса треугольника AMC
, то \frac{OM}{OC}=\frac{AM}{AC}
(см. задачу 1509), а так как \frac{AM}{AC}=\frac{2}{3}
, то
OM=\frac{2}{5}CM=8.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 22, с. 45
