536. В равнобедренном треугольнике радиус вписанной окружности составляет \frac{2}{7}
высоты, а периметр этого треугольника равен 56. Найдите его стороны.
Ответ. 16; 20; 20.
Указание. Центр окружности, вписанной в треугольник, — точка пересечения его биссектрис.
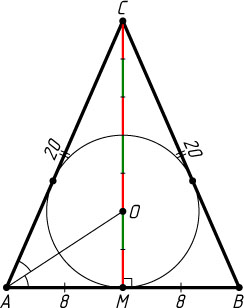
Решение. Пусть CM
— высота данного треугольника ABC
, AC=BC
, O
— центр вписанной окружности. Тогда OM
— радиус этой окружности, AO
— биссектриса треугольника AMC
. Поэтому
\frac{AC}{AM}=\frac{CO}{OM}=\frac{5}{2}
(см. задачу 1509). Поскольку AC+AM=28
, то
AC=20,~AM=8,~AB=16.
Источник: Шклярский Д. О., Ченцов Н. Н., Яглом И. М. Избранные задачи и теоремы элементарной математики. — Ч. 2: Геометрия (планиметрия). — М.: ГТТИ, 1952. — № 24, с. 46
