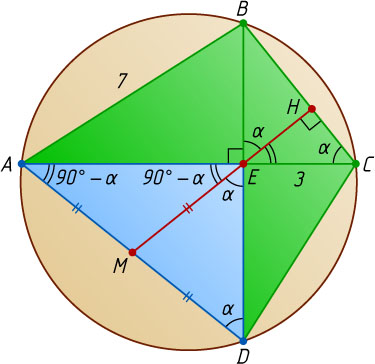
578. В окружность вписан четырёхугольник ABCD
, диагонали которого взаимно перпендикулярны и пересекаются в точке E
. Прямая, проходящая через точку E
и перпендикулярная к BC
, пересекает сторону AD
в точке M
. Докажите, что EM
— медиана треугольника AED
и найдите её длину, если AB=7
, CE=3
, \angle ADB=\alpha
.
Ответ. \frac{\sqrt{49-9\tg^{2}\alpha}}{2\sin\alpha}
.
Решение. Вписанные углы ACB
и ADB
опираются на одну и ту же дугу, поэтому
\angle ECB=\angle ACB=\angle ADB=\alpha.
Пусть прямые ME
и BC
пересекаются в точке H
. Тогда
\angle DEM=\angle BEH=\angle BCE=\alpha,
поэтому ME=MD
. Аналогично, ME=MA
. Следовательно, M
— середина AD
, т. е. EM
— медиана треугольника AED
(см. задачу 369).
Из прямоугольных треугольников BCE
, ABE
и AED
находим, что
BE=CE\tg\alpha=3\tg\alpha,~AE=\sqrt{AB^{2}-BE^{2}}=\sqrt{49-9\tg^{2}\alpha},
AD=\frac{AE}{\sin\alpha}=\frac{\sqrt{49-9\tg^{2}\alpha}}{\sin\alpha}.
Следовательно, EM=\frac{1}{2}AD=\frac{\sqrt{49-9\tg^{2}\alpha}}{2\sin\alpha}
.
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 25
Источник: Вступительный экзамен на факультет вычислительной математики и кибернетики (ВМК) МГУ. — 1979, № 3, вариант 3
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 13.28, с. 105
