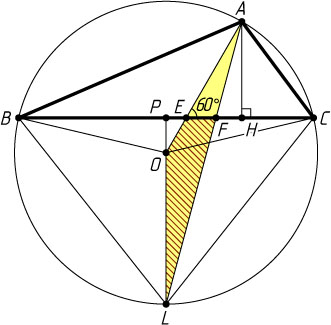
613. В окружность с центром O
вписан треугольник ABC
(\angle A\gt\frac{\pi}{2}
). Продолжение биссектрисы AF
угла A
этого треугольника пересекает окружность в точке L
, а радиус AO
пересекает сторону BC
в точке E
. Пусть AH
— высота треугольника ABC
. Известно, что AL=4\sqrt{2}
, AH=\sqrt{2\sqrt{3}}
, \angle AEH=\frac{\pi}{3}
.
а) Докажите, что AF
— биссектриса угла EAH
.
б) Найдите отношение площади треугольника OAL
к площади четырёхугольника OEFL
.
Ответ. \frac{4}{3}
.
Указание. Углы при основании равнобедренного треугольника AOL
равны 15^{\circ}
.
Решение. а) Биссектриса угла A
и серединный перпендикуляр к стороне BC
пересекаются в точке, лежащей на описанной окружности треугольника ABC
(см. задачу 1743), а треугольник AOL
равнобедренный, поэтому OL\parallel AH
. Тогда
\angle EAO=\angle OAL=\angle ALO=\angle LAH=\angle FAH.
Следовательно, AF
— биссектриса угла EAH
.
б) Из прямоугольных треугольников AHF
и AHE
и равнобедренного треугольника AOL
находим, что
AF=\frac{AH}{\cos\angle HAF}=\frac{\sqrt{2\sqrt{3}}}{\cos15^{\circ}},
AE=\frac{AH}{\cos\angle HAE}=\frac{\sqrt{2\sqrt{3}}}{\cos30^{\circ}}=\frac{\sqrt{2\sqrt{3}}}{\frac{\sqrt{3}}{2}}=\frac{2\sqrt{2\sqrt{3}}}{\sqrt{3}},
OA=OL=\frac{\frac{1}{2}AL}{\cos\angle OAL}=\frac{2\sqrt{2}}{\cos15^{\circ}}.
Тогда (см. задачу 3007)
S_{\triangle EAF}=\frac{AE}{AO}\cdot\frac{AF}{AL}S_{\triangle AOL}=\frac{\frac{2\sqrt{2\sqrt{3}}}{\sqrt{3}}}{\frac{2\sqrt{2}}{\cos15^{\circ}}}\cdot\frac{\frac{\sqrt{2\sqrt{3}}}{\cos15^{\circ}}}{4\sqrt{2}}\cdot S_{\triangle AOL}=\frac{1}{4}S_{\triangle AOL},
S_{OEFL}=S_{\triangle AOL}-S_{\triangle EAF}=\frac{3}{4}S_{\triangle AOL}.
Следовательно,
\frac{S_{\triangle AOL}}{S_{OEFL}}=\frac{S_{\triangle AOL}}{\frac{3}{4}S_{\triangle AOL}}=\frac{4}{3}.
Источник: Вступительный экзамен на геологический факультет МГУ. — (отделение геофизики) 1977, вариант 1, № 4
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 76
