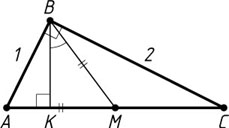
649. В треугольнике ABC
к стороне AC
проведены высота BK
и медиана MB
, причём AM=BM
. Найдите косинус угла KBM
, если AB=1
, BC=2
.
Ответ. \frac{4}{5}
.
Указание. Докажите, что данный треугольник — прямоугольный.
Решение. Поскольку BM=AM=MC
, то треугольник ABC
— прямоугольный (см. задачу 1188). Поэтому
AC=\sqrt{AB^{2}+BC^{2}}=\sqrt{5},~AC\cdot BK=AB\cdot BC,~BK=\frac{AB\cdot BC}{AC}=\frac{2}{\sqrt{5}},
BM=\frac{1}{2}AC=\frac{\sqrt{5}}{2},~\cos\angle KBM=\frac{BK}{BM}=\frac{4}{5}.
Источник: Вступительный экзамен на филологический факультет МГУ. — 1980 (отд. структурной и прикладной лингвистики), вариант 2, № 4
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 124
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 1.4, с. 10
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 2.21, с. 24
