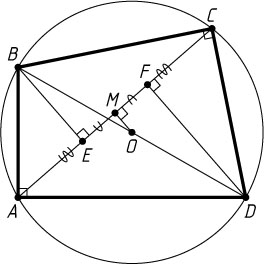
686. В выпуклом четырёхугольнике ABCD
противоположные углы A
и C
прямые. На диагональ AC
опущены перпендикуляры BE
и DF
. Докажите, что CE=FA
.
Указание. Опустите перпендикуляр из центра окружности, описанной около данного четырёхугольника, на диагональ AC
(далее см. задачу 1939).
Решение. Поскольку из точек A
и C
отрезок BD
виден под прямым углом, то точки A
и B
лежат на окружности с диаметром BD
. Опустим перпендикуляр OM
из центра O
этой окружности на диагональ AC
. Тогда AM=MC
и ME=MF
как проекции равных радиусов OB
и OD
на AC
(см. задачу 1939). Следовательно, CE=FA
.
Источник: Вступительный экзамен на экономический факультет МГУ. — 1972, № 4, вариант 3
Источник: Готман Э. Г., Скопец З. А. Решение геометрических задач аналитическим методом: Пособие для учащихся 9—10 кл. — М.: Просвещение, 1979. — № 245, с. 39
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 1.9, с. 12
