697. В окружность радиуса 3+2\sqrt{3}
вписан правильный шестиугольник ABCDEK
. Найдите радиус круга, вписанного в треугольник BCD
.
Ответ. \frac{3}{2}
.
Указание. Радиус окружности, вписанной в треугольник, равен площади треугольника, делённой на его полупериметр.
Решение. Пусть R
— радиус данной окружности. В треугольнике BCD
известно, что
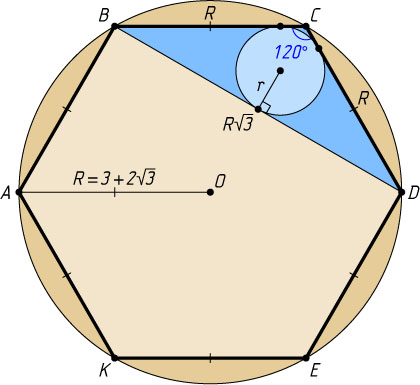
\angle BCD=120^{\circ},~BC=CD=R,~BD=R\sqrt{3},
S_{\triangle BCD}=\frac{1}{2}R^{2}\sin120^{\circ}=\frac{R^{2}\sqrt{3}}{4}.
Тогда радиус окружности, вписанной в этот треугольник, можно вычислить по формуле
r=\frac{2S_{\triangle BCD}}{BC+CD+BD}=\frac{\frac{R^{2}\sqrt{3}}{2}}{2R+R\sqrt{3}}=\frac{\frac{R\sqrt{3}}{2}}{2+\sqrt{3}}=\frac{\sqrt{3}(2\sqrt{3}+3)}{2(2+\sqrt{3})}=\frac{3}{2}
(см. задачу 452).
Источник: Вступительный экзамен на факультет почвоведения МГУ. — 1973, вариант 3, № 4
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 78
