710. В треугольнике ABC
отрезок MN
с концами на сторонах AC
и BC
параллелен основанию AB
и касается вписанной окружности. Предполагая, что углы A
и B
известны и равны соответственно 2\alpha
и 2\beta
, найдите коэффициент подобия треугольников ABC
и MNC
.
Ответ. \ctg\alpha\ctg\beta
.
Указание. Коэффициент подобия указанных треугольников равен отношению их полупериметров.
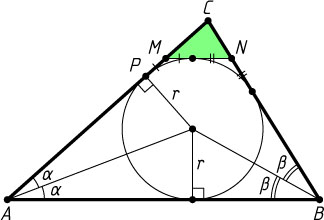
Решение. Пусть P
— точка касания вписанной окружности со стороной AC
, r
— радиус вписанной окружности. Тогда
AB=r\ctg\alpha+r\ctg\beta=r(\ctg\alpha+\ctg\beta),~AP=r\ctg\alpha,
PC=r\ctg\frac{1}{2}\angle C=r\ctg(90^{\circ}-\alpha-\beta)=r\tg(\alpha+\beta).
С другой стороны, отрезок PC
равен полупериметру треугольника MNC
, а полупериметр треугольника ABC
равен
r(\ctg\alpha+\ctg\beta+\tg(\alpha+\beta))
(см. задачу 4805).
Коэффициент подобия треугольников ABC
и MNC
равен отношению их полупериметров, т. е.
\frac{r(\ctg\alpha+\ctg\beta+\tg(\alpha+\beta))}{r\tg(\alpha+\beta)}=\ctg\alpha\ctg\beta.
Источник: Вступительный экзамен в МИИТ. — 1979
