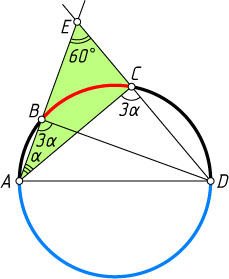
726. Четыре точки окружности следуют в порядке: A
, B
, C
, D
. Продолжение хорды AB
за точку B
и хорды CD
за точку C
пересекаются в точке E
, причём угол AED
равен 60^{\circ}
. Угол ABD
в три раза больше угла BAC
. Докажите, что AD
— диаметр окружности.
Указание. \angle ACD
— внешний угол треугольника ACE
.
Решение. Первый способ. Обозначим \angle BAC=\alpha
. Тогда \angle ABD=3\alpha
. Поскольку
\angle ACD=\angle ABD=3\alpha,
а \angle ACD
— внешний угол треугольника ACE
, то
\angle ACD=\angle BAC+\angle AED,~\mbox{т. е.}~3\alpha=\alpha+60^{\circ}.
Отсюда находим, что \alpha=30^{\circ}
, а \angle ABD=3\alpha=90^{\circ}
. Поэтому AD
— диаметр окружности.
Второй способ. Заметим, что
\angle AED=\frac{\cup AD-\cup BC}{2}
(см. задачу 27). Если \angle BAC=\alpha
, то имеем уравнение
60^{\circ}=\frac{6\alpha-2\alpha}{2}.
Откуда находим, что \alpha=30^{\circ}
. Следовательно,
\angle ABD=3\alpha=90^{\circ}.
Поэтому AD
— диаметр.
Источник: Вступительный экзамен на геологический факультет МГУ. — 1991, № 5, вариант 1
Источник: Журнал «Квант». — 1992, № 2, с. 60
