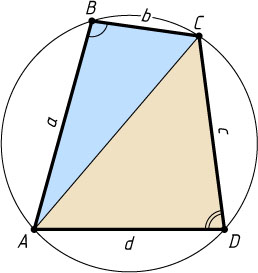
730. Формула Брахмагупты. Докажите, что если стороны вписанного четырёхугольника равны a
, b
, c
и d
, то его площадь S
может быть вычислена по формуле
S=\sqrt{(p-a)(p-b)(p-c)(p-d)},
где p=\frac{a+b+c+d}{2}
— полупериметр четырёхугольника.
Указание. Выразите квадрат диагонали AC
четырёхугольника ABCD
из треугольников ABC
и ADC
, учитывая, что \angle B+\angle D=180^{\circ}
, и найдите \cos\angle B
, а затем \sin\angle B
.
Решение. Первый способ. Пусть AC
— диагональ вписанного четырёхугольника ABCD
, AB=a
, BC=b
, CD=c
, AD=d
. Выразим AC^{2}
по теореме косинусов из треугольников ABC
и ADC
и, учитывая, что \angle B+\angle D=180^{\circ}
, получим:
a^{2}+b^{2}-c^{2}-d^{2}=2(ab+cd)\cos\angle B.
Тогда
\cos\angle B=\frac{a^{2}+b^{2}-c^{2}-d^{2}}{2(ab+cd)}~\Rightarrow~\sin^{2}\angle B=1-\left(\frac{a^{2}+b^{2}-c^{2}-d^{2}}{2(ab+cd)}\right)^{2}=
=\frac{(2ab+2cd)^{2}-(a^{2}+b^{2}-c^{2}-d^{2})^{2}}{4(ab+cd)^{2}}=
=\frac{(2ab+2cd-a^{2}-b^{2}+c^{2}+d^{2})(2ab+2cd+a^{2}+b^{2}-c^{2}-d^{2})}{4(ab+cd)^{2}}=
=\frac{((c+d)^{2}-(a-b)^{2})\cdot((a+b)^{2}-(c-d)^{2})}{4(ab+cd)^{2}}=
=\frac{(c+d-a+b)(c+d+a-b)(a+b-c+d)(a+b+c-d)}{4(ab+cd)^{2}}=
=\frac{4(p-a)(p-b)(p-c)(p-d)}{(ab+cd)^{2}}.
Следовательно,
S=S_{\triangle ABC}+S_{\triangle ADC}=\frac{1}{2}ab\sin\angle B+\frac{1}{2}cd\sin\angle D=\frac{1}{2}(ab+cd)\sin\angle B=
=\frac{1}{2}(ab+cd)\sqrt{\frac{4(p-a)(p-b)(p-c)(p-d)}{(ab+cd)^{2}}}=\sqrt{(p-a)(p-b)(p-c)(p-d)}.
Второй способ. См. задачу 3270.
Примечание. См. статью Д.Терёшина «Вписанный четырёхугольник», Квант, 1992, N2, с.37-39.
Источник: Журнал «Математика в школе». — 1991, № 5, с. 70. В.В.Прасолов. «Формула Брахмагупты»
Источник: Делоне Б. Н., Житомирский О. К. Задачник по геометрии. — М.—Л.: ОГИЗ, 1949. — № 250, с. 24
Источник: Коксетер Г. С. М., Грейтцер С. Л. Новые встречи с геометрией. — М.: Наука, 1978. — с. 73
Источник: Журнал «Квант». — 1992, № 2, с. 38
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 217, с. 63
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 514, с. 63
Источник: Готман Э. Г., Скопец З. А. Решение геометрических задач аналитическим методом: Пособие для учащихся 9—10 кл. — М.: Просвещение, 1979. — № 243, с. 38
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — с. 90
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 4.46(б), с. 86
