734. На сторонах AB
и AD
квадрата ABCD
взяты точки K
и M
так, что 3AK=4AM=AB
. Докажите, что прямая KM
касается окружности, вписанной в квадрат.
Указание. Проведите через точку K
касательную к окружности (отличную от KB
) и докажите, что она пересекает сторону AD
в точке M
.
Решение. Первый способ. Пусть сторона квадрата равна 1. По теореме Пифагора
KM=\sqrt{AK^{2}+AM^{2}}=\sqrt{\frac{1}{9}+\frac{1}{16}}=\frac{5}{12}.
Рассмотрим вневписанную окружность треугольника AKM
, касающуюся стороны MK
. Достаточно доказать, что эта окружность касается стороны AB
квадрата в её середине. Тогда это будет окружность, вписанная в квадрат.
Пусть P
— точка касания окружности с продолжением отрезка AK
, p
— полупериметр треугольника AKM
. Тогда (см. задачу 4805)
AP=p=\frac{1}{2}\left(\frac{1}{3}+\frac{1}{4}+\frac{5}{12}\right)=\frac{1}{2}.
Следовательно, P
— середина стороны AB
квадрата. Что и требовалось доказать.
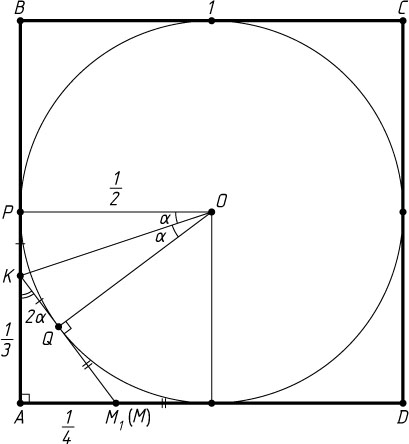
Второй способ. Пусть сторона квадрата равна 1, O
— центр окружности. Проведём через точку K
касательную к окружности, пересекающую сторону AD
в точке M_{1}
и касающуюся окружности в точке Q
. Пусть P
— середина AB
и \angle AKM_{1}=2\alpha
. Тогда
\angle QOP=\angle AKM_{1}=2\alpha,~\angle KOP=\alpha.
Поскольку
OP=\frac{1}{2},~KP=AP-AK=\frac{1}{2}-\frac{1}{3}=\frac{1}{6},
то
\tg\alpha=\frac{KP}{OP}=\frac{1}{3},~\tg2\alpha=\frac{2\tg\alpha}{1-\tg^{2}\alpha}=\frac{3}{4}.
Тогда
AM_{1}=AK\tg2\alpha=\frac{1}{3}\cdot\frac{3}{4}=\frac{1}{4},
т. е. точка M_{1}
совпадает с точкой M
.