746. Прямоугольный треугольник ABC
(\angle A=90^{\circ}
) и два квадрата BEFC
и AMNC
расположены так, что точки E
и A
лежат по разные стороны от прямой BC
, а точки M
и B
— по одну сторону от прямой AC
. Найдите расстояние между центрами квадратов, если AB=a
.
Ответ. \frac{a}{\sqrt{2}}
.
Указание. Пусть P
и Q
— центры данных квадратов. Докажите, что точки A
, P
и Q
лежат одной прямой.
Решение. Первый способ. Рассмотрим случай, когда AB\gt AC
. Пусть P
— центр квадрата BEFC
. Поскольку \angle BPC=\angle BAC=90^{\circ}
, то около четырёхугольника ABPC
можно описать окружность с диаметром BC
. Поскольку BP=PC
, то \angle BAP=\angle CAP=45^{\circ}
(см. задачу 805).
Обозначим BC=2R
, AC=b
. Тогда
AP=2R\sin\angle ABP=2R\sin(\angle ABC+\angle CBP)=2R\sin(\angle B+45^{\circ})=
=R\sqrt{2}\left(\frac{AC}{2R}+\frac{AB}{2R}\right)=\frac{AC+AB}{\sqrt{2}}=\frac{a+b}{\sqrt{2}}.
Пусть Q
— центр второго квадрата. Тогда \angle CAQ=45^{\circ}
. Поэтому точки A
, Q
и P
лежат на одной прямой, и в рассматриваемом случае точка Q
лежит между точками A
и P
. Следовательно,
QP=AP-AQ=\frac{a+b}{\sqrt{2}}-\frac{b}{\sqrt{2}}=\frac{a}{\sqrt{2}}.
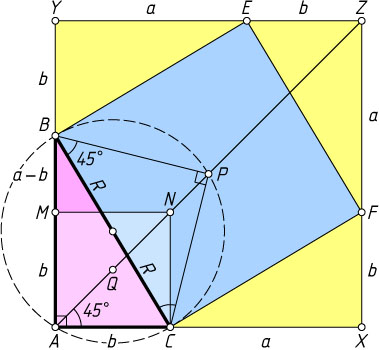
Второй способ. (Другой способ нахождения AP
.) Пусть X
— проекция точки F
на прямую AC
, а Y
— проекция точки E
на прямую AB
. Если Z
— точка пересечения прямых FX
и EY
, то AXZY
— квадрат со стороной a+b
, а AP
— половина его диагонали. Следовательно, AP=\frac{a+b}{\sqrt{2}}
.
Источник: Вступительный экзамен в МФТИ. — 1979, билет 11, № 3
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 79-11-3, с. 219
