756. Две окружности радиусов 1 и \sqrt{2}
пересекаются в точке A
. Расстояние между центрами окружностей равно 2. Хорда AC
большей окружности пересекает меньшую окружность в точке B
и делится этой точкой пополам. Найдите эту хорду.
Ответ. \sqrt{\frac{7}{2}}
.
Указание. Через центры окружностей проведите прямые, перпендикулярные хорде AC
.
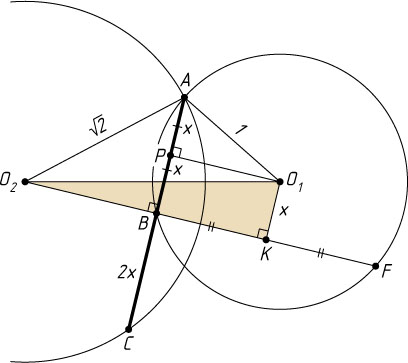
Решение. Первый способ. Пусть O_{1}
и O_{2}
— центры меньшей и большей окружностей соответственно, K
— проекция точки O_{1}
на прямую O_{2}B
, P
— проекция точки O_{1}
на прямую AC
, F
— точка пересечения луча O_{2}K
с меньшей окружностью. Тогда P
— середина AB
, а K
— середина BF
. Обозначим AP=x
. Тогда
O_{1}K=PB=x,~KB^{2}=O_{1}B^{2}-O_{1}K^{2}=1-x^{2},
O_{2}B^{2}=O_{2}A^{2}-AB^{2}=2-4x^{2}.
В прямоугольном треугольнике O_{1}KO_{2}
известно, что
O_{1}O_{2}=2,~O_{1}K=x,~O_{2}K=O_{2}B+KB=\sqrt{2-4x^{2}}+\sqrt{1-x^{2}}.
По теореме Пифагора
(\sqrt{2-4x^{2}}+\sqrt{1-x^{2}})^{2}+x^{2}=4.
Из этого уравнения находим, что x^{2}=\frac{7}{32}
. Следовательно, AC=4x=\sqrt{\frac{7}{2}}
.
Второй способ. Пусть O_{1}
и O_{2}
— центры меньшей и большей окружностей соответственно, K
— проекция точки O_{1}
на прямую O_{2}B
, P
— проекция точки O_{1}
на прямую AC
, F
— точка пересечения луча O_{2}K
с меньшей окружностью. Тогда P
— середина AB
, а K
— середина BF
.
Поскольку \angle ABF=90^{\circ}
, отрезок AF
— диаметр меньшей окружности. Тогда AF=2
. Обозначим \angle FAO_{2}=\alpha
. По теореме косинусов из треугольников O_{1}AO_{2}
и FAO_{2}
находим, что
\cos\alpha=\frac{AO_{1}^{2}+AO_{2}^{2}-O_{1}O_{2}^{2}}{2AO_{1}\cdot AO_{2}}=\frac{2+1-4}{2\cdot1\cdot\sqrt{2}}=-\frac{1}{2\sqrt{2}},
O_{2}F=\sqrt{AF^{2}+AO_{2}^{2}-2AF\cdot AO_{2}\cos\alpha}=\sqrt{4+2+2\cdot2\cdot\sqrt{2}\cdot\frac{1}{2\sqrt{2}}}=2\sqrt{2}.
Пусть прямая O_{1}O_{2}
пересекает меньшую окружность в точках M
и T
. Из точки O_{2}
проведены секущие O_{2}BF
и O_{2}TM
к меньшей окружности. Значит, O_{2}B\cdot O_{2}F=O_{2}T\cdot O_{2}M
(см. задачу 2636), откуда
O_{2}B=\frac{O_{2}T\cdot O_{2}M}{O_{2}F}=\frac{1\cdot3}{2\sqrt{2}}=\frac{1\cdot3}{2\sqrt{2}}.
По теореме Пифагора
AB=\sqrt{AO_{2}^{2}-O_{2}B^{2}}=\sqrt{2-\frac{9}{8}}=\frac{\sqrt{7}}{2\sqrt{2}}.
Следовательно,
AC=2AB=\sqrt{\frac{7}{2}}.
Третий способ. Пусть P
— середина хорды AB
. Тогда
\angle ABO_{2}=\angle APO_{1}=90^{\circ}
(см. задачу 1677).
Опустим перпендикуляр O_{1}K
на прямую O_{2}B
. Обозначим AP=PB=x
, O_{2}B=y
, KB=z
. Четырёхугольник O_{1}KBP
— прямоугольник, поэтому O_{1}P=KB=z
. Аналогично, O_{1}K=BP=x
. По теореме Пифагора из прямоугольных треугольников O_{1}PA
, ABO_{2}
и O_{1}KO_{2}
получаем
\syst{z^{2}+x^{2}=1\\4x^{2}+y^{2}=2\\x^{2}+(y+z)^{2}=2.\\}
Из первого уравнения системы выразим x^{2}=1-z^{2}
, а из первых двух уравнений — y^{2}=4z^{2}-2
, и подставим в третье уравнение. Получим
1-z^{2}+y^{2}+2yz+z^{2}=4,~\mbox{или}~1-z^{2}+4z^{2}-2+2yz+z^{2}=4,
откуда
y=\frac{5-4z^{2}}{2z}.
Тогда
4(1-z^{2})+\left(\frac{5-4z^{2}}{2z}\right)^{2}=2.
Из этого уравнения находим, что z^{2}=\frac{25}{32}
. Тогда
x^{2}=1-z^{2}=1-\frac{25}{32}=\frac{7}{32}.
Следовательно,
AC=4x=4\sqrt{\frac{7}{32}}=\sqrt{\frac{7}{2}}.
Источник: Вступительный экзамен в МФТИ. — 1978, билет 12, № 4
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 78-12-4, с. 210
Источник: Журнал «Crux Mathematicorum». — 1990, № 6, задача 4, с. 169
