758. Через вершины A
и C
треугольника ABC
проведена окружность K
, центр которой лежит на окружности, описанной около треугольника ABC
. Окружность K
пересекает продолжение стороны BA
за точку A
в точке M
. Найдите угол BCA
, если MA:AB=2:5
, а \angle ABC=\arcsin\frac{3}{5}
.
Ответ. \frac{\pi}{4}
.
Указание. Пусть AN
— высота треугольника ABC
. Докажите, что треугольник ANC
— равнобедренный.
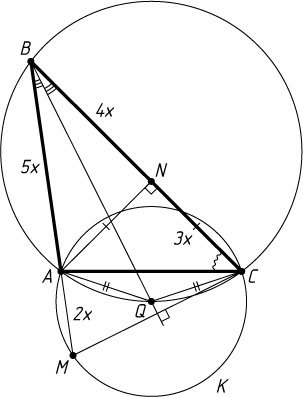
Решение. Пусть Q
— центр окружности K
, AB=5x
, AM=2x
, AN
— высота треугольника ABC
. Тогда
AN=AB\sin\angle ABC=3x,~BN=4x,
\angle AMC=\frac{1}{2}\angle AQC=\frac{1}{2}(180^{\circ}-\angle ABC)=90^{\circ}-\frac{1}{2}\angle ABC.
Поскольку QA=QC
, то BQ
— биссектриса угла ABC
(см. задачу 805). Поэтому \angle QBM=\frac{1}{2}\angle ABC
. Следовательно, MC\perp BQ
. Поэтому треугольник MBC
равнобедренный, BM=BC=7x
. Тогда
BC-BN=7x-4x=3x=NC.
Следовательно,
\angle BCA=\angle NCA=45^{\circ}.
