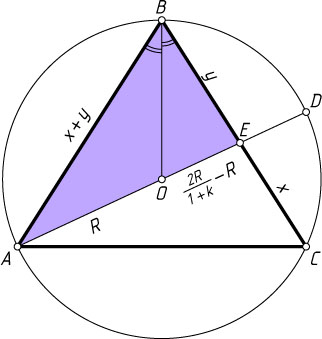
774. Равнобедренный треугольник ABC
(AB=BC
) вписан в окружность. Диаметр AD
пересекает сторону BC
в точке E
, при этом DE:EA=k
. Найдите отношение CE
к BC
.
Ответ. \frac{2k}{1+k}
.
Указание. Если O
— центр окружности, то BO
— биссектриса треугольника ABE
.
Решение. Обозначим CE=x
, BE=y
, R
— радиус окружности. Тогда AB=x+y
.
По условию \frac{DE}{AE}=k
и DE+AE=2R
. Следовательно,
AE=\frac{2R}{1+k}.
Пусть O
— центр окружности. Поскольку треугольник ABC
равнобедренный, то BO
— биссектриса треугольника ABE
. Тогда по свойству биссектрисы треугольника (см. задачу 1509)
\frac{AB}{BE}=\frac{AO}{OE},~\mbox{или}~\frac{x+y}{y}=\frac{R}{\frac{2R}{1+k}-R}.
Отсюда находим, что
\frac{x}{y}=\frac{2k}{1-k},~\frac{CE}{BC}=\frac{2k}{1+k}.
Источник: Вступительный экзамен в МФТИ. — 1972, билет 10, № 3
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 72-10-3, с. 156
