776. Окружность, вписанная в треугольник ABC
, делит медиану BM
на три равные части. Найдите отношение BC:CA:AB
.
Ответ. 5:10:13
.
Указание. Примените теорему о касательной и секущей и формулу для медианы через стороны треугольника.
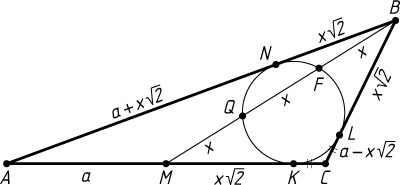
Решение. Пусть K
, L
и N
— точки касания вписанной окружности со сторонами AC
, BC
и AB
соответственно; F
и Q
— точки пересечения окружности с медианой BM
(F
— между B
и Q
). Предположим, что точка K
расположена между точками M
и C
. Обозначим BC=a
, BF=FQ=QM=x
. Тогда
BL^{2}=BQ\cdot BF=2x^{2}.
Поэтому BL=x\sqrt{2}
, BN=BL=x\sqrt{2}
. Аналогично находим, что KM=x\sqrt{2}
, а так как CL=CK
, то
MC=BC=a,~AC=2a,~AB=AN+NB=a+x\sqrt{2}+x\sqrt{2}=a+2x\sqrt{2}.
Выразим медиану BM
через стороны треугольника ABC
(см. задачу 4014):
4BM^{2}=2\cdot BC^{2}+2\cdot AB^{2}-AC^{2},~\mbox{или}
36x^{2}=2a^{2}+2(a+2x\sqrt{2})^{2}-4a^{2}.
Из этого уравнения находим, что a=\frac{5x\sqrt{2}}{4}
. Тогда
BC=a=\frac{5x\sqrt{2}}{4},~AC=2a=\frac{5x\sqrt{2}}{2},
AB=a+2x\sqrt{2}=\frac{13x\sqrt{2}}{4}.
Следовательно, BC:CA:AB=5:10:13
.
Примечание. Верно и обратное: в треугольнике со сторонами, пропорциональными числам 5, 10 и 13, медиана, проведённая из вершины среднего по величине угла, делится вписанной окружностью на три равные части.
Заметим, что такой треугольник существует, так как 5+10\gt13
. Пусть BC=5a
, AC=10a
, AB=13a
, а BM
— медиана треугольника ABC
. Тогда
BM=\frac{1}{2}\sqrt{2BC^{2}+2AB^{2}-AC^{2}}=\frac{1}{2}\sqrt{50a^{2}+338a^{2}-100a^{2}}=\frac{1}{2}a\sqrt{288}=6a\sqrt{2}.
Пусть вписанная окружность пересекает медиану BM
в точках E
и Q
и касается сторон BC
и AC
в точках L
и P
соответственно. Тогда
BL=\frac{AB+BC-AC}{2}=\frac{13a+5a-10a}{2}=4a.
Пусть K
— середина медианы BM
. Треугольник BCM
равнобедренный, поэтому K
— середина FQ
. Обозначим KF=KQ=t
. По теореме о касательной и секущей BF\cdot BQ=BL^{2}
, или
(3a\sqrt{2}-t)(3a\sqrt{2}+t)=16a^{2},~18a^{2}-t^{2}=16a^{2},
откуда t=a\sqrt{2}
. Следовательно,
FQ=2t=2a\sqrt{2},~BF=MQ=\frac{BM-FQ}{2}=\frac{6\sqrt{2}-2\sqrt{2}}{2}=2a\sqrt{2},
т. е. BF=FQ=MQ
.