4014. Стороны треугольника равны a
, b
, c
. Докажите, что медиана, проведённая к стороне c
, равна \frac{1}{2}\sqrt{2a^{2}+2b^{2}-c^{2}}
.
Указание. Достройте данный треугольник до параллелограмма.
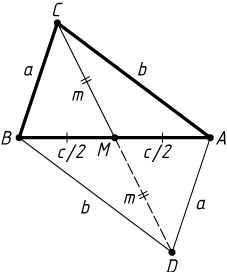
Решение. Пусть AB=c
, BC=a
, AC=b
— стороны треугольника ABC
; CM=m
— медиана треугольника.
На продолжении медианы CM
за точку M
отложим отрезок MD
, равный CM
. Тогда ACBD
— параллелограмм. Поэтому (см. задачу 4011)
CD^{2}+AB^{2}=2(AC^{2}+BC^{2}),~\mbox{или}~4m^{2}+c^{2}=2(a^{2}+b^{2}).
Отсюда находим, что
m^{2}=\frac{1}{4}(2a^{2}+2b^{2}-c^{2}).
